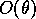 times the first-order forced response amplitude,
where
times the first-order forced response amplitude,
where 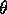 is the small parameter used in the analysis.
is the small parameter used in the analysis.
 R. Manasseh Papers
R. Manasseh Papers
 R. Manasseh Home
R. Manasseh Home
Copyright Cambridge University Press 1994.
Richard Manasseh
Department of Applied Mathematics and Theoretical Physics,
University of Cambridge,
Silver Street, Cambridge CB3 9EW, UK
Current affiliation: School of Mathematics, University of New South Wales,
Sydney, NSW 2052, Australia
In general, the system under consideration is the homogeneous fluid completely filling a spinning container, and subjected to some form of external forcing. The specific fluid system studied in this paper is contained in a right circular cylinder spinning steadily about its axis of symmetry. The fluid was supposed to have attained solid-body rotation before the commencement of forcing, in which there is initially no fluid motion relative to the container walls. The forcing was due to a small `precession' of the axis of spin: this axis itself rotated in inertial space to trace out the surface of a double cone. The apexes of these cones are together at the container centroid.
For inertial oscillations in a cylindrical container, the dispersion relation giving the eigenfrequencies of linear inviscid normal modes was first derived by Kelvin (1880) and its predictions for the eigenfrequencies were tested experimentally by Fultz (1959), McEwan (1970), Stergiopoulos & Aldridge (1982) and Manasseh (1992).
McEwan (1970) measured the amplitude of the oscillations using a thermistor probe. He found reasonable agreement of the amplitude - cylinder-height spectrum with the linear inviscid theory, near the lowest-order mode he could force. To do this he had to include modes with radial wavenumbers up to 5 in the theoretical spectrum. However, he found the resolution of the spectrum to be ``poor", responding essentially to the lowest order mode that could be forced.
Several experimental studies of rotating fluid systems in which inertial modes arise (for example Malkus 1968, McEwan 1970 and Manasseh 1992) have documented fluid flow breakdowns leading to turbulence. Manasseh (1992) described a system kinematically identical to the one in this paper, but made a wider and less detailed survey of the parameter space. Different breakdown regimes were catalogued by a letter scheme (A-G), where a Type A breakdown results in the generation of turbulence with the smallest scales. Manasseh (1992) described flow visualizations by means of a reflective flake technique that provided an excellent picture of the flow structure, but gave no information on fluid velocities. Quantitative data was extracted in the form of the times for the breakdowns to occur. The breakdown phenomena, while readily produced over a large region of parameter space, appeared to be complex and varied.
The cause or causes of the breakdowns remain unclear. There is some experimental evidence of nonlinear interactions between inertial modes in a cylinder (Aldridge and Stergiopoulos 1991; Manasseh 1992). In Aldridge and Stergiopoulos (1991) a least-squares procedure was used to recover the time-dependent eigenfrequencies corresponding to freely decaying modes in a cylindrical cavity. The decay rates of some modes were found to vary with time. An interpretation of this has the mode amplitudes slowly oscillating with time, due to nonlinear interactions. In Manasseh (1992) visual observations, quantified by image-processing measurements, were made of higher-order modes than those directly forced. Normally, such evidence would prompt the use of a weakly nonlinear or low-order dynamical systems model, based on a low number of modes. However, the inertial modes in a cylinder cannot be conveniently grouped into resonant triads, owing to the nature of their dispersion relation, preventing a simple implementation of weakly nonlinear theory. Furthermore, it is only in a small region of parameter space that a low number of modes appears to be interacting.
Some breakdown phenomena are associated with a mean flow taking the form of an
azimuthal circulation relative to the container walls. The participation of an
azimuthal circulation in resonant collapse was suggested by both McEwan (1970)
and Gunn and Aldridge (1990). Although linear inviscid theory predicts only
oscillatory flow under oscillatory forcing, wave-mean flow interactions (see,
for example, McIntyre and Norton 1990) occur when some dissipation and
nonlinearity are permitted. An asymptotic analysis by Thompson (1970) predicted
a small mean flow 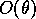 times the first-order forced response amplitude,
where
times the first-order forced response amplitude,
where 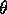 is the small parameter used in the analysis.
is the small parameter used in the analysis.
Recent interest in elliptical flow instabilities (Gledzer et al 1989; Malkus 1989; Waleffe 1990; Malkus & Waleffe 1991; Gledzer & Ponomarev 1992) has broadened the relevance of the inertia wave breakdown phenomena. An inertia wave mode can be shown (Waleffe 1990) to be the fastest growing unstable mode in the instability of an elliptical flow. It was suggested by Malkus & Waleffe (1991) that the subsequent breakdown of the inertial mode is an ``ubiquitous source of turbulence which by-passes lesser chaotic phases".
A practical application lies in the control of spinning spacecraft carrying liquid fuels, for which inertial oscillations and their prevention are of current research interest (Scott and Tan 1993, Manasseh 1993).
The first and main objective of the experiments reported here was to gain further insight into the flows reported in McEwan (1970) and Manasseh (1992), by using a different flow visualization technique that provides some information on the magnitudes of velocity in the flow. A specific aim was to determine if the dyeline pattern before breakdown corresponded to that predicted by linear inviscid theory. The experiments were to be conducted near the resonances of low-order modes, so that relatively simple structures should develop for easy comparison with theory. The single low-order mode closest to resonance was expected to dominate the flow - although other, high-order, modes would have resonances nearby owing to the unusual nature of the dispersion relation, these would be damped by viscosity. This paper is restricted to describing the experiments near the lowest-order mode that could be forced: the `fundamental' mode. A second objective, which was only partly met, was to determine if an azimuthal circulation was a significant participant in the breakdown of the flow.
The linear inviscid theory is presented in §2 in outline form only, since it has already been detailed in Manasseh (1992). The experimental techniques are described §3 and a guide to interpreting the experimental results is in §4. A description of a calculation used to compare the predictions of linear inviscid theory with the early stages of the experiments is in §5, while the actual experimental results are in §6.
Referring to figure 1, which defines some basic
parameters, consider a general fluid-filled container spinning about an axis
through its centroid and precessing about a second axis through its centroid.
Assume the centroid is not accelerating in inertial space, and the angle
between the two axes is not varying with time. In rotating fluid dynamics
problems one typically chooses the basic rotation period of the fluid relative
to inertial space as the time scale; in our problem this is 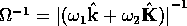 . Here,
however, we will choose the time scale to be
. Here,
however, we will choose the time scale to be 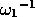 . In making this
choice of time scale, we are anticipating observing experiments from a frame of
reference in which periods of
. In making this
choice of time scale, we are anticipating observing experiments from a frame of
reference in which periods of 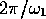 are easily counted to provide a time
scale with which various events can be measured. In fact, in the experiments to
be described later,
are easily counted to provide a time
scale with which various events can be measured. In fact, in the experiments to
be described later, 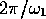 is the rotation period of the tank relative
to the observing cameras. The length scale
is the rotation period of the tank relative
to the observing cameras. The length scale 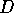 is equal to the container
diameter. The cylinder length/diameter aspect ratio is
is equal to the container
diameter. The cylinder length/diameter aspect ratio is 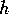 . We assume that the
nutation angle
. We assume that the
nutation angle 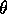 between the two axes is small, and assuming that
the velocity scale U
between the two axes is small, and assuming that
the velocity scale U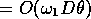 allows linearization of the
problem. The dimensional pressure is
allows linearization of the
problem. The dimensional pressure is 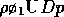 , where
, where 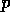 is the
dynamic pressure in excess of the centrifugal pressure that plays no dynamical
role in this problem. The nondimensional excitation frequency
is the
dynamic pressure in excess of the centrifugal pressure that plays no dynamical
role in this problem. The nondimensional excitation frequency 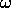 is
defined as twice the ratio of the basic rotation rate
is
defined as twice the ratio of the basic rotation rate 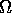 to first order
in
to first order
in 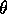 , to the frequency of the variation of the overall angular velocity
vector in tank co-ordinates,
, to the frequency of the variation of the overall angular velocity
vector in tank co-ordinates, 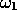 , giving
, giving
The incompressible inviscid linearized fluid equation of motion relative to axes fixed in the container is
together with continuity,
Equation (2) is the form of the momentum equation appropriate to our problem; steps in its derivation are outlined in Wood (1966). The boundary condition is
where 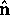 is the unit normal vector to the container surface.
This allows a free-slip condition at the container wall consistent with the
assumption of an inviscid flow. To effect the inviscid approximation, an
Ekman number, defined by
is the unit normal vector to the container surface.
This allows a free-slip condition at the container wall consistent with the
assumption of an inviscid flow. To effect the inviscid approximation, an
Ekman number, defined by 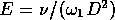 , has been assumed to
be negligibly small. The dimensional spin-up time is given by
, has been assumed to
be negligibly small. The dimensional spin-up time is given by
Adopt
cylindrical polar co-ordinates 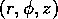 fixed in the tank, with their
origin at the cylinder centroid.
Assuming a separable solution to the homogeneous version of (2),
of form
fixed in the tank, with their
origin at the cylinder centroid.
Assuming a separable solution to the homogeneous version of (2),
of form
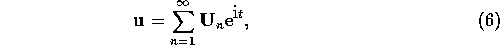
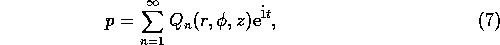
and eliminating the velocity components with the aid of the continuity equation, we get Poincaré's equation,
a hyperbolic p.d.e. for  . The associated boundary condition is
. The associated boundary condition is
In an unbounded domain (8) admits a set of plane-wave solutions, which are usually referred to in the literature as inertia waves. Although the full problem given by (8) and (9) is ill-posed, it is possible to find an analytic description of the flow in the case of the particular geometry of a right circular cylinder.
For brevity, the index  is used to indicate a unique combination of the
spatial wavenumbers
is used to indicate a unique combination of the
spatial wavenumbers 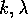 and
and 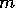 . The integer
. The integer 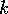 is the axial
wavenumber and the integer
is the axial
wavenumber and the integer 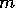 is the azimuthal wavenumber. As the radial
wavenumber
is the azimuthal wavenumber. As the radial
wavenumber 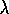 is non-integer, it is convenient to use an integer index
is non-integer, it is convenient to use an integer index
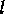 to count the number of half-cycles in the radial direction.
to count the number of half-cycles in the radial direction.
A solution to (8) and (9) by separation of variables is
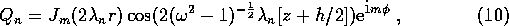
where 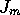 is the Bessel function of the
first kind, order
is the Bessel function of the
first kind, order 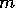 .
A solution to Poincaré's equation of this kind was
first found by Kelvin (1880).
.
A solution to Poincaré's equation of this kind was
first found by Kelvin (1880).
Resonant excitation frequencies
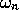 correspond to eigenvalues of the system for this particular geometry and
for precessional forcing, which requires modes with
correspond to eigenvalues of the system for this particular geometry and
for precessional forcing, which requires modes with 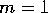 .
Some of the lower order
.
Some of the lower order 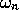 are tabulated below for the
cylinder length / diameter ratio
are tabulated below for the
cylinder length / diameter ratio 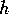 of this experiment.
of this experiment.
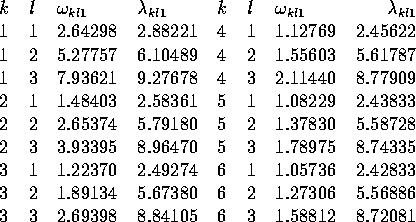
Table 1: Resonant excitation frequencies 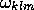 and radial wavenumbers
and radial wavenumbers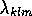 for a precessionally forced cylinder,
for a precessionally forced cylinder, 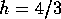
Note that the 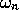 do not increase monotonically with
increasing order of the wavenumber vector. The
do not increase monotonically with
increasing order of the wavenumber vector. The 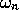 are densely spaced; for any
are densely spaced; for any 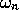 , it is possible to
find another arbitrarily close.
, it is possible to
find another arbitrarily close.
The velocity field
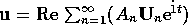 that solves (2),
is given by
that solves (2),
is given by
and the pressure by
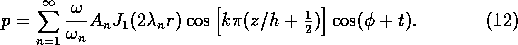
The amplitudes 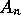 are found by calculating the inner-product
integral of the forcing function which is on the right-hand side of
(2), using the spatial structure of the
are found by calculating the inner-product
integral of the forcing function which is on the right-hand side of
(2), using the spatial structure of the  th mode. The calculation of
the
th mode. The calculation of
the 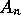 are presented in the Appendix to this paper.
are presented in the Appendix to this paper.
In principle we could force all the linear inviscid modes, up to the order
where the wavelength is comparable to the boundary layer thickness. However,
the modes that can be precessionally forced have 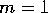 , as noted above.
Furthermore, the forcing function,
, as noted above.
Furthermore, the forcing function, 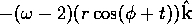 , is even in
, is even in  , so the modes upon which it will project must have a
vertical velocity that is also even in
, so the modes upon which it will project must have a
vertical velocity that is also even in  , requiring, from
(11), an odd axial wavenumber
, requiring, from
(11), an odd axial wavenumber 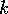 . As in Manasseh (1992), Low-order modes are those with a small wavenumber vector magnitude.
. As in Manasseh (1992), Low-order modes are those with a small wavenumber vector magnitude.
Full details of the apparatus and technique are in Manasseh (1991).
Figure 1 is a schematic diagram of the apparatus
which realized the precessing tank system. The perspex tank is of internal
diameter 90 mm and internal height 120 mm. It spins in a gimbal frame which is
in turn mounted on a turntable. Here 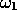 is the spin rate of the tank
relative to the gimbal frame and the precession rate
is the spin rate of the tank
relative to the gimbal frame and the precession rate 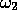 is the spin
rate of the turntable relative to the laboratory. The nutation angle
is the spin
rate of the turntable relative to the laboratory. The nutation angle 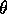 can be varied by tilting the gimbal frame from the vertical. For the
experiments reported in this paper, the tank spin axis was precessed at a
constant
can be varied by tilting the gimbal frame from the vertical. For the
experiments reported in this paper, the tank spin axis was precessed at a
constant 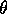 which was small (1
which was small (1 ). To do this, the system was
first spun up to a desired combination of
). To do this, the system was
first spun up to a desired combination of 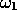 and
and 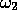 , with
, with 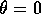 .
Precession, and hence forcing, was initiated by an impulsive tilt of the gimbal
frame to the preset value of 1
.
Precession, and hence forcing, was initiated by an impulsive tilt of the gimbal
frame to the preset value of 1 . The fluid was illuminated by a
diffuse fluorescent light source and viewed by a video camera or a still camera
fixed on the turntable.
. The fluid was illuminated by a
diffuse fluorescent light source and viewed by a video camera or a still camera
fixed on the turntable.
The experiments were performed at the Department of Applied Mathematics and Theoretical Physics (DAMTP) at Cambridge University. A DAMTP precision turntable was used; it is driven by a permanent magnet D.C. servomotor controlled by an analog loop, feedback being provided by an integral tachogenerator. The reference voltage is supplied by a BBC microcomputer with 16 bits resolution, which also controlled the experimental procedure for the experiments reported here.
The thymol blue electrolytic dyeline technique (Baker 1966) utilises
the colour change of thymol blue indicator molecules in the presence of a local
concentration of base ions. Thymol blue crystals are first dissolved in the
fluid, which is distilled water. The fluid is then made into an appropriate
electrolyte by the addition of acid and base solutions. This ambient fluid is
orange-yellow in colour. If a low (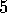 to
to 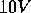 ) potential is applied to the
fluid by electrodes, H
) potential is applied to the
fluid by electrodes, H ions will collect at the cathode, forming a local
deficit of OH
ions will collect at the cathode, forming a local
deficit of OH ions which react with the indicator molecules to form a
dark blue dyed zone. If the applied voltage is switched off, the indicator will
eventually revert to its original colour; the technique can thus be used
continuously in a small fluid volume. In the meantime, fluid motion carries the
dyed patch away from the cathode, permitting a visualization of the flow.
ions which react with the indicator molecules to form a
dark blue dyed zone. If the applied voltage is switched off, the indicator will
eventually revert to its original colour; the technique can thus be used
continuously in a small fluid volume. In the meantime, fluid motion carries the
dyed patch away from the cathode, permitting a visualization of the flow.
A stainless steel wire of diameter 0.05 mm were used as the cathode. In the
experiments reported in this paper, a single wire was used. It was mounted
slant-wise in the tank with the ends of the wire mounted on the flat end-walls
of the cylinder at a radius of 12.5 mm. The anode was a single brass screw at
one end of the tank at a radius of 12.5 mm. A slanting orientation was chosen
so that both axial and horizontal velocities would cause a noticeable departure
of dye from the wire. Trial estimations of fluid velocity, made as described in
§6, gave fluid flows of order  relative to the wire, corresponding to a Reynolds number for the wire of about
relative to the wire, corresponding to a Reynolds number for the wire of about
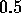 . Laminar vortex shedding from a cylinder does not begin until the
Reynolds number gets to about 50. Thus, in respect of spurious oscillatory
disturbances, the wire has a negligible influence on the flow. In the
visualizations there was no evidence of vortices being shed from the wire. The
possibility of other influences from the wire is discussed at the end of
§sec-5.1. Experiments in the (1,1,1) mode range and in §7.
. Laminar vortex shedding from a cylinder does not begin until the
Reynolds number gets to about 50. Thus, in respect of spurious oscillatory
disturbances, the wire has a negligible influence on the flow. In the
visualizations there was no evidence of vortices being shed from the wire. The
possibility of other influences from the wire is discussed at the end of
§sec-5.1. Experiments in the (1,1,1) mode range and in §7.
The experiments of McEwan (1970) and Manasseh (1992), which both used a reflective flake technique, reported difficulties in achieving solid-body rotation. In Manasseh (1992) a ``bright column" along the cylinder axis was noted, implying a relative shear in the fluid after several spin-up times had elapsed. The reflective flakes are aligned by any strain field above the level of that due to Brownian motion, irrespective of the magnitude of the velocities involved, and so the magnitude of the flow corresponding to the `bright column' was uncertain. Initial tests using the thymol blue technique indicated that the bright column present before the commencement of forcing did in fact correspond to a small anticyclonic departure from solid-body rotation. This departure was called the `anomaly drift' (Manasseh 1991). Careful calibrations were performed. (These included a study of the very slow `intrinsic' drift of the dyeline in a motionless tank that was probably due to the asymmetry in the electric field.) Optimal setting were found that minimized the anomaly drift and rendered the intrinsic drift negligible. In Manasseh (1991) the anomaly drift was shown to be at most 1/100 of the forced flow velocity and it was ascribed to small irregularities in the container spin rate. It was inferred that the behaviour in a system free of anomaly drifts was unlikely to be different, given a forced flow velocity typically 100 times larger.
The procedure during the experiments reported in §6 was as follows:
The tank was set spinning for about 2 hours. Tests had shown that the anomaly drift reduced to a stable value after about 2 hours.
The tank spin rate 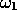 was stroboscopically checked and set using
an analog controller. The tank was left spinning throughout the set of
experimental runs.
was stroboscopically checked and set using
an analog controller. The tank was left spinning throughout the set of
experimental runs.
The procedure during each run was as follows:
1 The tank spin and turntable axes were set to be collinear. The turntable was spun up to a speed calculated by the microcomputer.
2 The theoretical spin-up time given by (5) was allowed to pass.
3 An additional period elapsed to ensure that any flows from a previous run had dissipated. The total wait time was at least 100 revolutions of the tank in inertial space, about 4 spin-up times for experiments conducted near the (1,1,1) mode resonant frequency.
4 The video recorder began recording. The dyeline current was switched on for 60 seconds, which was the optimum time determined by tests detailed in Manasseh (1991).
5 The gimbal locking catch was released to initiate forcing.
6 The turntable was spun down and the axes returned to collinear.
There were 4 runs at the same parameter settings to ensure repeatability of the results.
We can deduce how the dyeline should appear from the turntable frame of
reference from which the video recordings were made and the photographs taken.
The approximations of linearity and inviscid flow are still being made. The dye
particles, under the influence of forced inertia wave modes, should follow
orbital paths relative to tank-fixed co-ordinates, just as particles in the
ocean trace out orbital paths under the influence of surface gravity waves. The
dye particles should rotate on their orbits with the forcing frequency 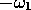 relative to tank-fixed co-ordinates, while the tank and wire fixed in it are
rotating relative to the camera with the opposite frequency,
relative to tank-fixed co-ordinates, while the tank and wire fixed in it are
rotating relative to the camera with the opposite frequency, 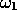 .
Figure 2 is a idealized diagram of this motion, near
the tank ends where the motion is essentially normal to the axis. The `radius'
of the orbits (idealized as circular) will increase as the amplitude of the
oscillation increases. As with any forced linear oscillator, the amplitude
depends linearly on the forcing amplitude and inversely on the closeness to
resonance. The wire that generated the dyeline is marked with a +. The dye
particles will be initially displaced from the wire during the impulsive
tilt-out that began the forcing. After this initial displacement (which will be
a slight curve since 0.1 s is about 1/6 of a rotation period and the Coriolis
force will have time to act) the particles will start to trace out an orbit
with a radius appropriate to the forced amplitude.
.
Figure 2 is a idealized diagram of this motion, near
the tank ends where the motion is essentially normal to the axis. The `radius'
of the orbits (idealized as circular) will increase as the amplitude of the
oscillation increases. As with any forced linear oscillator, the amplitude
depends linearly on the forcing amplitude and inversely on the closeness to
resonance. The wire that generated the dyeline is marked with a +. The dye
particles will be initially displaced from the wire during the impulsive
tilt-out that began the forcing. After this initial displacement (which will be
a slight curve since 0.1 s is about 1/6 of a rotation period and the Coriolis
force will have time to act) the particles will start to trace out an orbit
with a radius appropriate to the forced amplitude.
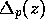 for a particular
for a particular
 , projected onto the plane imaged by the camera in the turntable or
precessing frame of reference, from which the exposures
(figures 5(a-h)) were taken. The tank, viewed from
above, is rotating clockwise in this frame of reference. Orbits of the
particles, shown for simplicity as circular, without the influence of free
modes and neglecting Stokes drift, are drawn at eight positions relative to the
turntable-fixed camera. The horizontal arrows show
, projected onto the plane imaged by the camera in the turntable or
precessing frame of reference, from which the exposures
(figures 5(a-h)) were taken. The tank, viewed from
above, is rotating clockwise in this frame of reference. Orbits of the
particles, shown for simplicity as circular, without the influence of free
modes and neglecting Stokes drift, are drawn at eight positions relative to the
turntable-fixed camera. The horizontal arrows show 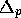 .
(a) View of particles near the top of the tank,
which initially tilts away from the camera,
thus the initial displacement (at position 1) relative to the wire is towards
to camera;
.
(a) View of particles near the top of the tank,
which initially tilts away from the camera,
thus the initial displacement (at position 1) relative to the wire is towards
to camera; 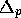 is to the left.
(b) View of particles near the bottom of the tank,
which initially tilts towards the camera; the initial displacement
(position 1, noting that base of the wire at the bottom is almost diametrically
opposite its base at the top) is away from the camera;
is to the left.
(b) View of particles near the bottom of the tank,
which initially tilts towards the camera; the initial displacement
(position 1, noting that base of the wire at the bottom is almost diametrically
opposite its base at the top) is away from the camera; 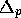 is to the
right.
is to the
right.
If the orbits were circular, and centred on the wire, the displacements of the dye particles from the wire, projected onto the plane viewed by the camera, would be perfectly constant, because the time dependence of their orbital motion is perfectly cancelled by that of the camera. However, even a circular orbit would not be centred on the wire. There are at least three reasons for this, under linear inviscid theory alone. Firstly, the forced-motion orbit's `centre' is not at the wire; as shown in figure 2, the steady orbital trajectory passes close to the wire since the particles start off there. Secondly, superimposed on the forced motion is the transient response, or free-mode `ringing', whose amplitude depends only on the magnitude of the initial tilt-out. The free mode with the largest amplitude is the one with the spatial structure closest to the form of the initial disturbance, namely, the (1,1,1) mode. Thus this largest free mode response closely resembles the forced response in structure; also, it oscillates with a natural frequency which is close to the forcing frequency, because the (1,1,1) mode is being forced near resonance. Thirdly, as with the surface gravity wave paradigm, there is a `Stokes drift' of the orbits. Because of the linear solution's three-dimensional velocity field (sinusoidal and Bessel functions,) a particle finds itself in a slightly different part of the velocity field on the completion of each orbit. (For simplicity, the free-modal response and `Stokes drift' are not shown on figure 2.)
Nevertheless, on the plane imaged by the camera fixed on the turntable, the displacement of the dyeline from on the wire should not appear to reverse sign in an oscillatory fashion. This is because, as noted above, the oscillatory time dependence of the dye particles in tank co-ordinates is precisely the same as that of the imaged plane; the camera in effect `follows' the dye particles around on their orbits.
The residual apparent motion of the dye particles relative to the wire on the
imaged plane should be that owing to the eccentricity of the orbit centres due
to the initial displacement, the beating between the forced and free modes and
the `Stokes drift'. All these influences, as well as the `radius' of the orbit
(which is steady once a steady forcing regime is established), are ultimately
related to the forced mode amplitudes (or directly to the size of the initial
tilt, upon which the forced mode amplitudes depend). Thus the distance,
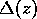 , of the dyeline from the wire, projected onto an
, of the dyeline from the wire, projected onto an  -
- plane
fixed in turntable co-ordinates, (where it is called
plane
fixed in turntable co-ordinates, (where it is called 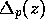 ), will
ultimately depend on
), will
ultimately depend on 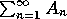 , where
, where 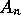 is the amplitude
of each mode. However, the dependence will not be simple because of the
complicating kinematic factors just mentioned. Near resonance of a low-order
mode, that mode should dominate the sum. It is possible to estimate
is the amplitude
of each mode. However, the dependence will not be simple because of the
complicating kinematic factors just mentioned. Near resonance of a low-order
mode, that mode should dominate the sum. It is possible to estimate 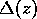 from
from 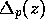 , and hence get a measure characteristic of what we presume
to be
, and hence get a measure characteristic of what we presume
to be 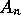 , where
, where  is the index of the low-order mode near resonance, to
within about
is the index of the low-order mode near resonance, to
within about 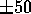 %, by viewing the video recordings of the spinning tank.
%, by viewing the video recordings of the spinning tank.
From §2 the axial structure of the flow
field near the resonance of a low-order mode should be sinusoidal with argument
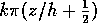 , and hence
, and hence 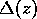 will have this dependence on
will have this dependence on  .
From the point of view of the camera (a side view in the turntable frame), the
dyeline should initially appear to tilt, as the fluid particles are displaced
relative to the tank by its initial tilt-over and by the resulting Coriolis
acceleration. This tilt should be modified by the free and forced modes of
oscillation; when, as in the experiments to be described, these modes are
dominated by the (1,1,1) mode, the tilt should appear as one-half of a
sine wave with a zero at the tank centroid.
.
From the point of view of the camera (a side view in the turntable frame), the
dyeline should initially appear to tilt, as the fluid particles are displaced
relative to the tank by its initial tilt-over and by the resulting Coriolis
acceleration. This tilt should be modified by the free and forced modes of
oscillation; when, as in the experiments to be described, these modes are
dominated by the (1,1,1) mode, the tilt should appear as one-half of a
sine wave with a zero at the tank centroid.
Linear inviscid calculations were made (summarized in the Appendix to
this paper and detailed in Manasseh (1991)), which permit an accurate
prediction of the forced response to be made. Precise comparisons of a
predicted linear flow field with these experiments are not possible, for two
reasons. Firstly, the rough nature of the estimation of the experimental
response, with its associated uncertainty of about 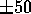 %, precludes a
precise comparison and probably befits best a scale comparison, which will be
given in §6. Secondly, the
comparison must be made on the basis of a few seconds' observation - within a
few revolutions of the commencement of forcing - since the flow appears to
irreversibly distort after this time. Despite these caveats, a numerical
calculation of the dyeline displacement
is still useful because it serves to highlight both the initial similarities
and the later differences that develop between the structure of the
predicted linear inviscid response and that in the actual experiment.
%, precludes a
precise comparison and probably befits best a scale comparison, which will be
given in §6. Secondly, the
comparison must be made on the basis of a few seconds' observation - within a
few revolutions of the commencement of forcing - since the flow appears to
irreversibly distort after this time. Despite these caveats, a numerical
calculation of the dyeline displacement
is still useful because it serves to highlight both the initial similarities
and the later differences that develop between the structure of the
predicted linear inviscid response and that in the actual experiment.
The basis of the calculation is an integration of the ordinary differential equations (11) for the forced fluid velocity, giving the path of a passive tracer particle under the influence of inertia wave modes. Several particles are started along the actual co-ordinates of the wire in the tank, and their positions at successive one-revolution periods are joined to form a simulation of the dyeline seen in the experiment.
The time taken for the initial tilt was about 0.1 s. The actual mechanical
arrangement causing the tilt-out was a spring with a pneumatic damper. The
damper was adjusted so that the motion was just underdamped; it reached the
preset 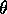 without any overshoot or jarring. Thus this brief tilting
motion is modelled by the first quarter-period of a sine function that
reaches its peak at 0.1 s.
without any overshoot or jarring. Thus this brief tilting
motion is modelled by the first quarter-period of a sine function that
reaches its peak at 0.1 s.
The calculation also incorporates some reckoning of the transient response, or free-mode `ringing', owing to the initial impulse that sets up the forcing. (In inviscid theory this ringing continues forever, but since only a tenth or so of the viscous decay timescale is being considered, an inviscid model seems appropriate for the free-mode response.) The precise value of the initial impulse given in the experiment could not be measured and could only be roughly inferred from the calibrations in Manasseh (1991). Further details are in the Appendix.
The predicted dyeline displacement is shown in figure 3. Although the calculation and plot are in tank co-ordinates, the orientation of the wire has been chosen to approximate its instantaneous orientation in the earliest experimental photographs reproduced in §6.
The first `dyeline' plotted is the locus of particle displacements at the first one-half period after the initial tilt; at this time and after successive one-period intervals the particles appear close to their maximum projected displacements for the chosen orientation, making it easier to discern the axial flow structure. Further details on the calculation are in the Appendix. In figure 4, we have `zoomed-in' on figure 3 to make individual pathlines more clear. In this end-view projections only the topmost pathline has been plotted. From this viewpoint the particles are moving anti-clockwise on their orbital paths. The advective drift or `Stokes drift' can be noted in these end-view projections.
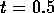 revolution, to match the estimated time of the first photograph,
figure 5(a). The actual co-ordinates of the experimental
wire have been used; slight departures from symmetry of the pathlines in the
top and bottom halves of the tank are due to the wire not passing through the
tank centroid, owing to experimental constraints.
revolution, to match the estimated time of the first photograph,
figure 5(a). The actual co-ordinates of the experimental
wire have been used; slight departures from symmetry of the pathlines in the
top and bottom halves of the tank are due to the wire not passing through the
tank centroid, owing to experimental constraints.
Figure:
Expanded view of one of the pathlines looking from the end of the
cylinder. The pathline shown is the topmost one in
figure 3. As in
figure 3, the reversed sense of the co-ordinates
is due to the rotation of the plot to give approximately the same phase of the
wire as in the earliest experimental photographs.
Initial trials were conducted with 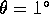 and near the (1,1,1) mode
resonance, to study the behaviour of the thymol dyeline. It was generated as
part of the computer-controlled experimental sequence. These trials determined
that nutation angles greater than
and near the (1,1,1) mode
resonance, to study the behaviour of the thymol dyeline. It was generated as
part of the computer-controlled experimental sequence. These trials determined
that nutation angles greater than 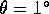 forced the system with too
large an amplitude for the dyeline technique to be of much use; the fluid
response was sufficient to sweep the dye away from the wire before it had a
chance to form a dyeline. Furthermore, if the forcing frequency was too close
to a resonance, dye was swept away from the wire even before the experiment
could begin, since there was always some small nonzero
forced the system with too
large an amplitude for the dyeline technique to be of much use; the fluid
response was sufficient to sweep the dye away from the wire before it had a
chance to form a dyeline. Furthermore, if the forcing frequency was too close
to a resonance, dye was swept away from the wire even before the experiment
could begin, since there was always some small nonzero 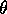 because of
unavoidable inaccuracies in the equipment. The trials were conducted near the
resonant frequency of the (1,1,1) mode,
because of
unavoidable inaccuracies in the equipment. The trials were conducted near the
resonant frequency of the (1,1,1) mode, 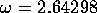 , and established the working range,
, and established the working range, 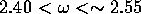 , of
, of 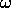 values near the (1,1,1) mode
resonance over which the thymol dyeline technique could be used to observe the
forced behaviour beyond a few revolutions. Presumably equally good
visualizations would have been obtained with frequencies equally far above the
resonant peak as the lower limit of the working range is below it; however it
was not practical to operate the apparatus at the very highest such speeds.
Some experiments were run at
values near the (1,1,1) mode
resonance over which the thymol dyeline technique could be used to observe the
forced behaviour beyond a few revolutions. Presumably equally good
visualizations would have been obtained with frequencies equally far above the
resonant peak as the lower limit of the working range is below it; however it
was not practical to operate the apparatus at the very highest such speeds.
Some experiments were run at 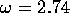 and
and 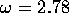 but it was judged unsafe
to conduct a lengthy series of experiments at the corresponding speeds.
but it was judged unsafe
to conduct a lengthy series of experiments at the corresponding speeds.
Experiments in this working range were then performed in order to address the
aims of §1. A series of experiments was conducted at
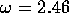 , 2.5, 2.54, 2.74 and 2.78. The nutation angle was set at
, 2.5, 2.54, 2.74 and 2.78. The nutation angle was set at
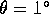 .
There were four runs at each
.
There were four runs at each 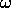 with identical settings. A more detailed
survey of the parameter space near this (1,1,1) mode resonance had been
planned. However, it turned out that the richness of the phenomena observed for
this limited number of points in parameter space, meant that the observation
and description of much more data would have been an overwhelming task.
with identical settings. A more detailed
survey of the parameter space near this (1,1,1) mode resonance had been
planned. However, it turned out that the richness of the phenomena observed for
this limited number of points in parameter space, meant that the observation
and description of much more data would have been an overwhelming task.
The dominant feature of all the dyeline experiments is the rapid development of structures that cannot be described by the linear inviscid theory of §2. Further experiments were conducted near the (3,1,1) and (5,2,1) mode resonances, which it is hoped will be presented in a future paper. With the (5,2,1) mode in particular it is hard to select any features that seem compatible with a linear inviscid response. Nevertheless, at early times after the commencement of forcing near the (1,1,1) mode resonance, the time dependence and structure of the dyeline displacement seem to be consistent with a linear inviscid description.
Therefore, estimates were made of the displacement 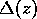 , near the tank
ends
, near the tank
ends 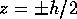 where
where 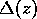 is initially a maximum. This was thought to
be characteristic of the amplitude of what was postulated to be the (1,1,1)
mode under linear inviscid theory. The estimate was made in the first few
revolutions after the commencement of forcing, from the experiments recorded at
is initially a maximum. This was thought to
be characteristic of the amplitude of what was postulated to be the (1,1,1)
mode under linear inviscid theory. The estimate was made in the first few
revolutions after the commencement of forcing, from the experiments recorded at
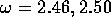 and 2.78 . There was considerable uncertainty in which time, if
any, was the correct one at which to make these estimates. After a few
revolutions the structure begins to irreversibly distort, and during this brief
time it is hard to say if there is a steady displacement of the dyeline from
the wire. Owing to this uncertainty the error in estimating the dyeline
displacement at this early stage was about
and 2.78 . There was considerable uncertainty in which time, if
any, was the correct one at which to make these estimates. After a few
revolutions the structure begins to irreversibly distort, and during this brief
time it is hard to say if there is a steady displacement of the dyeline from
the wire. Owing to this uncertainty the error in estimating the dyeline
displacement at this early stage was about 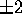 mm, about 50%. Estimates
were also made from the initial trials at
mm, about 50%. Estimates
were also made from the initial trials at 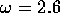 , before the dyeline at this
frequency became too faint to be discerned. The best visualizations were
obtained at
, before the dyeline at this
frequency became too faint to be discerned. The best visualizations were
obtained at 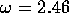 .
.
The behaviour at 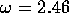 is illustrated by photographs, figures
5(a-h). Here, the microcomputer controlling the experiment
was programmed to take an exposure every revolution, beginning immediately
after the impulsive tilt. The uncertainty in the time
is illustrated by photographs, figures
5(a-h). Here, the microcomputer controlling the experiment
was programmed to take an exposure every revolution, beginning immediately
after the impulsive tilt. The uncertainty in the time 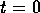 , caused by human
error in simultaneously initiating the tilt and microcomputer sequence, is
about
, caused by human
error in simultaneously initiating the tilt and microcomputer sequence, is
about 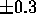 seconds (
seconds (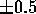 revolutions). The first photograph was
therefore at
revolutions). The first photograph was
therefore at 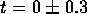 s or
s or 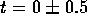 revolutions. The phase of the wire
relative to the camera at the commencement of forcing is random.
revolutions. The phase of the wire
relative to the camera at the commencement of forcing is random.
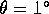 ,
,
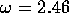 .
The spinning tank is being viewed from the turntable. (a) was
taken at about
.
The spinning tank is being viewed from the turntable. (a) was
taken at about 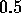 revolution
after the impulsive tilt, the remainder at
approximately 2 revolution intervals. (The exposures were taken approximately
every revolution; every second exposure has been reproduced here.) Slight
shifts in phase of the wire are due to inaccuracies in the timing of the
camera's motor drive. A dark vertical stripe near the tank bottom in some
photographs is a shadow from a small internal crack in the tank wall.
revolution
after the impulsive tilt, the remainder at
approximately 2 revolution intervals. (The exposures were taken approximately
every revolution; every second exposure has been reproduced here.) Slight
shifts in phase of the wire are due to inaccuracies in the timing of the
camera's motor drive. A dark vertical stripe near the tank bottom in some
photographs is a shadow from a small internal crack in the tank wall.
After the commencement of forcing, the dyeline moves away from the wire,
initially appearing like a straight line but tilted away from the wire at the
tank top and bottom. This state is shown in figure 5(a), taken
immediately after the commencement of forcing at 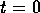 . (It is probable, given
the extent of development of the dyeline displacement in this first photograph,
that it was taken close to the
. (It is probable, given
the extent of development of the dyeline displacement in this first photograph,
that it was taken close to the 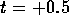 revolution limit of the error band
revolution limit of the error band
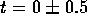 revolution.)
As noted in §4, the dyeline tilt
is due to a combination of the displacement of the fluid following the impulse
that initiated the forcing, the displacement due to the Coriolis acceleration
during the time the impulsive motion was occurring and the displacements caused
by the forced and free modes of oscillation and the `Stokes drift'.
revolution.)
As noted in §4, the dyeline tilt
is due to a combination of the displacement of the fluid following the impulse
that initiated the forcing, the displacement due to the Coriolis acceleration
during the time the impulsive motion was occurring and the displacements caused
by the forced and free modes of oscillation and the `Stokes drift'.
In the images of figure 5(a-h), the top of the tank and the wire fixed to it have been tilted away from the camera (and the bottom towards it). The dyeline is thus displaced from the wire towards the camera in the top half of the tank (and away from the camera in the bottom half). Since the camera continues to rotate from left to right relative to the tank, the dyeline always appears to tilt to the left in the top half of the tank (and to the right in the bottom half), as suggested schematically by figure 2. The net displacement does seem to be one-half of a sine wave with a zero at the tank centroid. Moreover, the displacement of the dyeline relative to the wire at this stage does not reverse sign (nor show any discernable oscillation) in the turntable (camera) frame of reference, since as expected it has the same frequency as the forcing. Thus the initial observation is consistent with the linear response dominated by the (1,1,1) mode predicted in §4.
It was at this early stage that the estimates of the amplitude were made, by
viewing video recordings. The tilted dyeline corresponds to the dyeline
particles tracing out roughly circular trajectories in tank co-ordinates, at
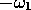 , opposite to the frequency of the tank relative to the turntable,
, opposite to the frequency of the tank relative to the turntable,
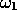 , with maxima in the dimensions of the orbits near the tank ends. From
the video recordings (see the earliest datapoints in
figure 6, which will be described later),
the dimension
, with maxima in the dimensions of the orbits near the tank ends. From
the video recordings (see the earliest datapoints in
figure 6, which will be described later),
the dimension 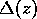 of these orbits at
of these orbits at 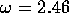 is
about
is
about  mm near the tank ends
mm near the tank ends 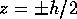 where the maximum azimuthal
and radial velocities should occur and do appear to occur initially. From this
dimension, assumed, from the argument in §4, to be characteristic of the orbit diameter, the fluid
velocity can be estimated. The orbital path length is about
where the maximum azimuthal
and radial velocities should occur and do appear to occur initially. From this
dimension, assumed, from the argument in §4, to be characteristic of the orbit diameter, the fluid
velocity can be estimated. The orbital path length is about 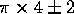 mm
mm 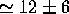 mm. The velocity of fluid particles is therefore
mm. The velocity of fluid particles is therefore
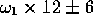 mm
mm 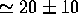 mm s
mm s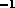 . This velocity is
consistent with the scale assumed under linear behaviour, which gives
U
. This velocity is
consistent with the scale assumed under linear behaviour, which gives
U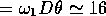 mm s
mm s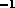 .
.
A periodic variation in the displacement of the dyeline from the wire could not
be confidently discerned. Recall, from §4, that this variation is due to the eccentricity of the orbit centres
owing to the initial displacement, the beating between the forced and free
modes and the `Stokes drift'. Measurements (shown in
figure 6) were made from the video images
of the dyeline displacement
(which is 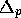 ,
, 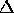 projected onto the imaged plane) at
half-revolution intervals. However, the developing instability about to be
described begins after a few revolutions, precluding any statistical confidence
in the couple of measurements that may be in the linear inviscid regime.
projected onto the imaged plane) at
half-revolution intervals. However, the developing instability about to be
described begins after a few revolutions, precluding any statistical confidence
in the couple of measurements that may be in the linear inviscid regime.
Figure:
Projected displacement
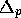 (in mm) of the dye from the wire,
measured from the video images, for
(in mm) of the dye from the wire,
measured from the video images, for 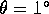 ,
, 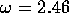 , as a
function of time
, as a
function of time 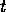 (in revolutions). The measurements were made relative to
the wire near the bottom of the tank (at
(in revolutions). The measurements were made relative to
the wire near the bottom of the tank (at 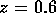 ), hence, in the first few
revolutions, the dye particles are displaced to the right (positive
), hence, in the first few
revolutions, the dye particles are displaced to the right (positive
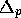 ), as shown in figure 2(b).
), as shown in figure 2(b).
 : the displacement to the furthest discernable limit of the dyeline,
when the wire is on the right of the image, and
: the displacement to the furthest discernable limit of the dyeline,
when the wire is on the right of the image, and  : on the left. The
measurements have not been corrected for optical distortion from the circular
tank wall or the video screen.
: on the left. The
measurements have not been corrected for optical distortion from the circular
tank wall or the video screen.
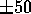 %, at each of
%, at each of 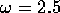 ,
, 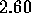 ,
, 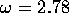 and at
and at 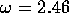 .
.
In the experiments, the dyeline does not remain approximately fixed in shape as
predicted by linear inviscid theory and as illustrated by numerical
calculations based on such theory. Figures 5(b-h) show the later
development; they are at 2 revolution intervals, with figure 5(b)
being at about 2.5 revolutions and figure 5(h) at about 14.5
revolutions. After about 5 revolutions (3 seconds in real time), a `kink'
begins to develop in the dyeline which, in the course of the next few
revolutions, develops into an `S' shape, i.e. a function that is odd in
 with an axial wavenumber of approximately 3/2. This `kink' of the dyeline
away from the wire at the tank centre plane is where linear inviscid theory
predicts the minimum displacement.
In addition, this new `kink' structure rotates with the tank, and hence
is non-oscillatory in tank co-ordinates. This is in contrast to the
linear-theoretical response, which should appear approximately steady in the
turntable (forcing) frame of reference since it is oscillatory in tank
co-ordinates. The video recordings clearly show that the new development
becomes three-dimensional, resembling two half-turns of a corkscrew. By 14.5
revolutions (figure 5 h) the upper and lower arms of the dyeline
have wound up into spiral forms. All the details described above seem to be
perfectly repeatable.
with an axial wavenumber of approximately 3/2. This `kink' of the dyeline
away from the wire at the tank centre plane is where linear inviscid theory
predicts the minimum displacement.
In addition, this new `kink' structure rotates with the tank, and hence
is non-oscillatory in tank co-ordinates. This is in contrast to the
linear-theoretical response, which should appear approximately steady in the
turntable (forcing) frame of reference since it is oscillatory in tank
co-ordinates. The video recordings clearly show that the new development
becomes three-dimensional, resembling two half-turns of a corkscrew. By 14.5
revolutions (figure 5 h) the upper and lower arms of the dyeline
have wound up into spiral forms. All the details described above seem to be
perfectly repeatable.
In figure 6 measurements are shown of the
displacement of the dyeline from the wire, at half-revolution intervals. After
about 5 revolutions (3 seconds) the measured displacements on either side of
the tank diverge, owing to the enticement of the dye into the new
non-oscillatory `kink flow' that can be observed developing from this time. If
the motion had remained according to linear inviscid theory, the datapoints
from the left- and right-hand sides would each have followed a straight line at
constant 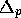 , modulated by a beating with the free modes and the Stokes
drift.
, modulated by a beating with the free modes and the Stokes
drift.
The velocity of fluid displacement causing the kink is an initial
maximum of  , since it reaches a radius of about
, since it reaches a radius of about
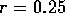 (22 mm) in about 10 revolutions (6 seconds). This should be compared
with about
(22 mm) in about 10 revolutions (6 seconds). This should be compared
with about  for the oscillatory modal response. The
non-oscillatory motion of the kink does not imply that all oscillatory motion
in the tank has ceased, rather, that a non-oscillatory flow (which is able to
cause a net transport of dye) has arisen in addition to the oscillatory flow.
The flow causing the kink appears to arrest after about 10 revolutions,
when the more complicated `winding up' of the dyeline arms is noted.
for the oscillatory modal response. The
non-oscillatory motion of the kink does not imply that all oscillatory motion
in the tank has ceased, rather, that a non-oscillatory flow (which is able to
cause a net transport of dye) has arisen in addition to the oscillatory flow.
The flow causing the kink appears to arrest after about 10 revolutions,
when the more complicated `winding up' of the dyeline arms is noted.
This `winding up' appearance can be traced to striations in the dyelines, first visible in figure 5(d), which begin near the centre of the tank. It is in this region where the fluid velocities are smallest under linear inviscid theory, being zero at the centroid. If an influence from the wire were to generate the striations (by vortex shedding for example) this would be expected to be in a region where velocities are more substantial. Furthermore, an influence from the wire would be expected to manifest itself first where flows are closer to normal to the wire, where the wire presents more of an obstacle. The regions of the tank where flows are close to normal to the wire are at the ends of the tank. Again this is away from the centre where the striations are first seen.
The axial nature of the striations, or `winding-up' appearance of the dyelines, is noteworthy, as is the spread of these small-scale features throughout the tank. Possibly they represent the spread of turbulent eddies as the flow becomes more disordered. Eddies in rotating flows would be expected to exhibit a strong axial orientation. The `Type B' breakdown (Manasseh 1992) that occurs for the parameters of the present experiments is characterized in part by small-scale axially-oriented features.
Although the kink is a visually dramatic departure from the linear inviscid description, it should be remembered that its velocity is at most 20% of the linear response. Structures like the kink were not noted by McEwan (1970) and Manasseh (1992). This can be ascribed to the nature of the reflective flake visualization technique they used. As the spatial gradients in the `kink flow' and the (1,1,1) mode flow appear similar, we can infer that their strain fields, which align the reflective flakes, are in the same approximate ratio as their velocity fields, i.e. about 1/5. The kink was probably not noted because it corresponds to a weak strain distribution rotating with the tank. Any such strain distribution will only be noted as it passes through the sheet of light (see Manasseh 1992 for details) illuminating a reflective flake experiment. Unless the kink is really a manifestation of a perfectly axisymmetric flow, it should appear as a weak flickering of the reflected image, with a frequency equal to the rotation rate of the tank relative to the turntable (or to some multiple of it, if the kink structure has many radial planes of symmetry). Moreover, as the `kink flow' arrests after about 10 revolutions, its strain distribution should appear as a weak flickering that persists for only about 10 revolutions, perhaps explaining why it was not noted in McEwan (1970) Manasseh (1992).
Experiments previously conducted in the current working range, with the
reflective flake visualization technique (Manasseh 1992), had determined that
the typical breakdown expected for 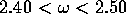 was a long timescale
instability manifesting itself in the order of 100 revolutions. For
was a long timescale
instability manifesting itself in the order of 100 revolutions. For 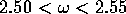 Type B collapses occur, again in the order of 100 revolutions. At
Type B collapses occur, again in the order of 100 revolutions. At 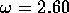 a Type A collapse was noted to occur in the order of 50 revolutions. Type
A collapses result in the generation of turbulence with eddy scales about a
tenth of the tank diameter, whereas Type B collapses result in a weakly
turbulent flow and appear to be preceded by interactions with higher-order
modes. The dyelines generated at
a Type A collapse was noted to occur in the order of 50 revolutions. Type
A collapses result in the generation of turbulence with eddy scales about a
tenth of the tank diameter, whereas Type B collapses result in a weakly
turbulent flow and appear to be preceded by interactions with higher-order
modes. The dyelines generated at 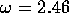 had dissipated by about 50
revolutions after the commencement of forcing, making further visualization
impossible; dyelines generated at
had dissipated by about 50
revolutions after the commencement of forcing, making further visualization
impossible; dyelines generated at 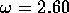 had dissipated by about 10
revolutions. Therefore, in these dyeline experiments, the dyelines had
dissipated before the `resonant collapse' instability as identified by the
reflective flake technique had manifested itself.
had dissipated by about 10
revolutions. Therefore, in these dyeline experiments, the dyelines had
dissipated before the `resonant collapse' instability as identified by the
reflective flake technique had manifested itself.
It was not possible to generate dyelines at later stages during the experimental run, because, as noted in §3.2, a period of about 60 seconds without any flow was needed to generate a dyeline. Had the current been switched on when flow was being forced, dye would have been swept away from the wire too rapidly for a dyeline to be formed.
The repeatablilty of the kink formation raises the possibilty that it is wholly or in part associated with some geometric feature of the tank, the forcing regime or with a systematic fault in the experiment. It was in part to address this concern that further experiments were done with higher modes, to see if the kink still occurs at other forcing frequencies. It does not; for the (3,1,1) mode, for example, equal departures from the linear inviscid prediction begin at three points, corresponding exactly to the intersection of the axis with the three nodal planes where velocities normal to the axis are identically zero according to the linear theory for the (3,1,1) mode. (In fact, the (1,1,1)-mode kink occurs at the single nodal plane of the (1,1,1) mode.) More complex structures occur for still higher modes, without the presence of a clear kink as with the (1,1,1) mode. As with the (1,1,1)-mode results, these observations are easily repeatable.
The fact that quite different anomalies arise at different forcing frequencies (with the tank geometry and the amplitude and structure of the forcing function identical) suggests that the kink does not arise from a geometric flaw or some fault in the experimental procedure. It is hoped that experiments with other modes will be reported in a future paper.
The primary aim of this series of experiments was to examine the dyeline pattern before a breakdown had occurred and to see if it is consistent with the predictions of linear inviscid theory. It is, albeit for only a few revolutions; a measure characteristic of the flow amplitude has the correct scale and the time dependence is oscillatory in tank co-ordinates as expected. However, a `kink' soon develops in the linear inviscid dyeline structure. It is a manifestation of a flow that is not oscillatory and has a velocity about 1/5 of the estimated linear component of the response.
It is conceivable that the kink in the dyeline originates in the viscous terms
neglected in the simple analysis of §2, either in an Ekman
or Stewartson layer effect or even in some interaction with the visualization
wire itself. Also, discontinuities on characteristic surfaces are predicted in
contained rotating fluids (Wood 1966) which may have a physical realization as
extensions of the viscous boundary layers into the interior. If viscous forces
are at work, we expect the flows they represent to be of 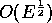 times
the first-order inviscid amplitude. This is about
times
the first-order inviscid amplitude. This is about 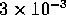 times the
first-order inviscid amplitude. For the experiment in §6 a measure characteristic of this amplitude was estimated to be about
20 mm s
times the
first-order inviscid amplitude. For the experiment in §6 a measure characteristic of this amplitude was estimated to be about
20 mm s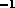 , giving viscous flows of order
, giving viscous flows of order  .
However, the flow that produced the kink in figure 5(e) had a
magnitude of order 1 mm s
.
However, the flow that produced the kink in figure 5(e) had a
magnitude of order 1 mm s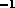 . This is one and a half to two orders of
magnitude larger than a viscous mechanism would predict. There is not enough
precise data to rule out a viscous mechanism for producing the kink, but on the
basis of its order of magnitude that seems an improbable cause.
. This is one and a half to two orders of
magnitude larger than a viscous mechanism would predict. There is not enough
precise data to rule out a viscous mechanism for producing the kink, but on the
basis of its order of magnitude that seems an improbable cause.
A secondary aim was to determine if a large mean flow (corresponding, say, to a
circulation of order 0.1 times the basic spin 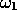 as suggested by Gunn and
Aldridge (1990)) was present. However, even the small mean flow calculated by
Thompson (1970) was not observed. This is now to be expected as it is
as suggested by Gunn and
Aldridge (1990)) was present. However, even the small mean flow calculated by
Thompson (1970) was not observed. This is now to be expected as it is 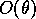 times the first-order forced response amplitude, and since a measure
characteristic of this amplitude is about 20 mm s
times the first-order forced response amplitude, and since a measure
characteristic of this amplitude is about 20 mm s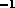 , the second-order mean
flow should be about 0.2 mm s
, the second-order mean
flow should be about 0.2 mm s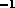 . Thus over the 5 revolutions or so before
the kink appeared, about 3 seconds in real time, the dyeline would only have
moved about 0.6 mm, too small to be clearly distinguished from the flow due to
the first-order forced response. It was not possible to generate a first order
forced response sufficiently large for a noticeable second-order flow to
develop.
. Thus over the 5 revolutions or so before
the kink appeared, about 3 seconds in real time, the dyeline would only have
moved about 0.6 mm, too small to be clearly distinguished from the flow due to
the first-order forced response. It was not possible to generate a first order
forced response sufficiently large for a noticeable second-order flow to
develop.
In conclusion, the use of the dyeline technique has suggested that linear inviscid theory for contained inertia waves has some validity, for a very brief period following the commencement of forcing, both in its prediction of the scale of flow velocity and of the flow's oscillatory time dependence. However the experiments have also revealed the formation of a structure not explained by linear theory, which develops before the collapses detailed in Manasseh (1992), indeed within a few revolutions of the commencement of forcing.
A mean circulation could be invoked to explain this or other breakdown phenomena. However, some mechanism is needed to explain how a mean circulation can interact with the inertia wave modes, and grow larger than the second-order level permitted by formal asymptotic theory (Thompson 1970).
Further experiments were carried out to test ideas that the `kink' originated in a weakly nonlinear interaction with a mode that cannot be forced under linear theory. It is hoped that these, along with the results of experiments near the resonances of higher order modes and further discussion and speculation on the nature of these instabilities will be presented in future papers.
I did this work while a PhD student in the Department of Applied Mathematics and Theoretical Physics, University of Cambridge. I owe thanks to my supervisor, Dr. Paul Linden, as well as to my colleagues, in particular Drs. David Tan, Michael McIntyre and John Jackson, for many helpful discussions. This work was done as part of a project funded by the British National Space Centre / Royal Aerospace Establishment and managed by British Aerospace PLC. I should like to acknowledge the support of those organizations. Some of the final numerical calculations needed for figure 3 were done on a Sequent Symmetry S27 computer at the School of Mathematics of the University of New South Wales.
Firstly it is shown how the linear steady-state velocity field resulting from an
applied, single frequency forcing can be estimated by summing a series of
inertia wave modes, with their amplitudes calculated by a `mode projection'
approach. A mode projection approach to calculating the amplitudes of forced
inertial oscillations in a cylinder was first described in the unpublished
thesis of Kudlick (1966), though numerical calculations based on it were not
required for comparisons with experiment. This approach could be contrasted
with the `inhomogeneous boundary condition' method. The inhomogeneous boundary
condition method expresses the disturbance pressure as a Fourier series in  ,
from which the velocity field can be derived. It is detailed in Tan (1991). In
the mode projection approach, the projection of the applied force field onto a
particular mode is calculated. Each of these modes individually satisfies
the homogeneous boundary conditions. Then the responses or projections of
all possible modes, when appropriately recombined, should reproduce the force
field. Although mathematically standard and straightforward, as detailed in
Manasseh (1991), neither approach, when realized numerically, is without its
pitfalls; the difficulties may be related to the ill-posedness of the original
problem defined by (2) and (3).
,
from which the velocity field can be derived. It is detailed in Tan (1991). In
the mode projection approach, the projection of the applied force field onto a
particular mode is calculated. Each of these modes individually satisfies
the homogeneous boundary conditions. Then the responses or projections of
all possible modes, when appropriately recombined, should reproduce the force
field. Although mathematically standard and straightforward, as detailed in
Manasseh (1991), neither approach, when realized numerically, is without its
pitfalls; the difficulties may be related to the ill-posedness of the original
problem defined by (2) and (3).
Secondly, the free mode response is estimated, based on the measurements of the initial impulse in Manasseh (1991), and the velocity field is integrated to determine a number of particle paths.
To begin a calculation based on the mode projection approach, first establish some identities by considering once more the homogeneous form of (2),
with incompressibility and the homogeneous boundary condition 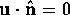 , where
, where
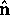 is the outward unit vector normal to the surface. For
special values of
is the outward unit vector normal to the surface. For
special values of 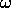 , say
, say 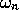 , (13) is satisfied with a single mode of
the form
, (13) is satisfied with a single mode of
the form
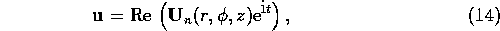
where
 corresponds to a combination of spatial wavenumbers that is unique to each
mode. Then (13) becomes
corresponds to a combination of spatial wavenumbers that is unique to each
mode. Then (13) becomes
Following Greenspan (1968) we can arrange the following expressions from
(16), where 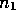 and
and 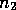 represent different modes:
represent different modes:
where  denotes complex conjugation.
Now consider the integrals of (17) and (18) over the container volume.
First note that
denotes complex conjugation.
Now consider the integrals of (17) and (18) over the container volume.
First note that
because of the incompressibility condition. Then
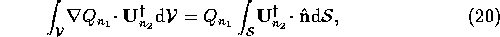
by Gauss's theorem, where 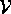 is the container volume and
is the container volume and 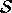 is its surface. Then,
because of the boundary condition,
is its surface. Then,
because of the boundary condition,
As
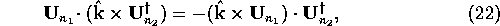
integrating (17) and (18) over the volume and adding them gives
so that
and therefore, from the integral of (17) and from (21),
i.e. the functions 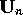 must be orthogonal.
Now define the inner product operation as
must be orthogonal.
Now define the inner product operation as
where X
is any complex vector function of 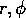 and
and  .
Applying this operation to (16) gives
.
Applying this operation to (16) gives
because of (21), (24) and (25). Hence
Now consider the inhomogeneous problem
where 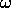 is prescribed and does not coincide with any of the
is prescribed and does not coincide with any of the 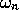 ,
together with incompressibility and boundary conditions.
Assume a solution to (29) of the form
,
together with incompressibility and boundary conditions.
Assume a solution to (29) of the form
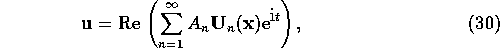
which upon substitution into (29) gives
which, noting from
(16) that 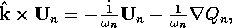 becomes
becomes
Now applying the inner product operation gives
using (21) to eliminate the pressure
term. Thus, if the 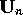 are a complete set and the
are a complete set and the 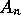 are calculated
according to (34), from (33) the
are calculated
according to (34), from (33) the 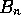 are given by
are given by
Referring to §2, recall that the spatial structure 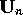 of a mode is given by (11),
of a mode is given by (11),
The forcing term F from the right-hand side of the inhomogeneous equation
for precessional forcing (2) is
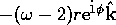 . To calculate
. To calculate 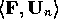 ,
therefore, it is necessary to evaluate the integral
,
therefore, it is necessary to evaluate the integral
Now calculate
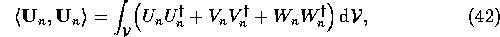
where, using (38),
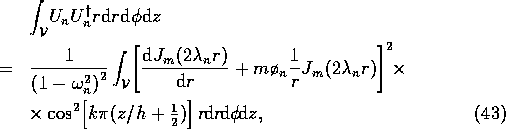
where
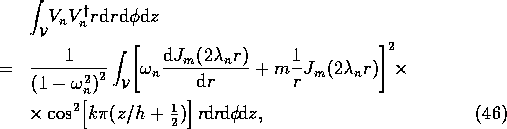
where
and
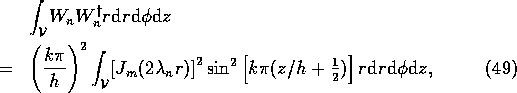
by using the standard properties of Bessel functions. On adding (44), (47) and (50),
and so, from (33), (41) and (51),
the amplitude of the  th mode is given by
th mode is given by
From (38), the velocity
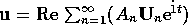 is given by
is given by
and the pressure by
Here we consider the determination of the fluid particle pathlines corresponding to a sum of linear inviscid modes. These modes comprise some of the forced modes, and the free mode with the largest amplitude.
Given the linear inviscid solution, the problem of calculating the fluid
pathlines is twofold; firstly, the integrals giving 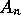 in (52)
must be calculated, and secondly, we must solve the three nonlinearly coupled
ordinary differential equations (38) for
in (52)
must be calculated, and secondly, we must solve the three nonlinearly coupled
ordinary differential equations (38) for 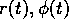 and
and
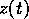 . Numerical Algorithms Group (NAG) routines were used throughout, coded
in double-precision FORTRAN and run on the Cambridge IBM 3084.
. Numerical Algorithms Group (NAG) routines were used throughout, coded
in double-precision FORTRAN and run on the Cambridge IBM 3084.
The integrals in the term 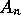 were calculated
with a third-order finite difference scheme. The solution of
(38) was done numerically with an adjustable stepsize
Runge-Kutta routine. The paths were calculated for dye particles released
as passive tracers at a succession of points along a hypothetical wire.
were calculated
with a third-order finite difference scheme. The solution of
(38) was done numerically with an adjustable stepsize
Runge-Kutta routine. The paths were calculated for dye particles released
as passive tracers at a succession of points along a hypothetical wire.
The actual motion during the tilt-out is modelled by making the nutation angle
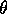 a function of time for the 0.1 s taken by the tilting motion. As noted
in §5, the mechanical origin of the tilting motion leads this displacement to
be modelled as first quarter-period of a sine function that reaches its peak at
0.1 s.
a function of time for the 0.1 s taken by the tilting motion. As noted
in §5, the mechanical origin of the tilting motion leads this displacement to
be modelled as first quarter-period of a sine function that reaches its peak at
0.1 s.
Fourteen forced modes are included in the calculation; they are tabulated in table A.2. It was found that for the parameters of the experiments reported here, the (1,1,1) mode, which was being forced near resonance, so dominated the response that it accounted for 90-95% of the velocity field.
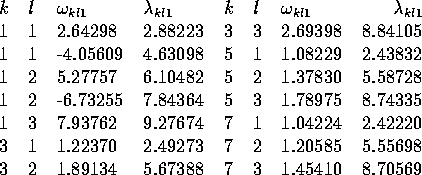
Table 2: Modes used in the forced response calculation
It was decided that one free mode, the (1,1,1) mode, should be included since its structure best represents the initial tilt disturbance applied to the system. The free mode's response was only estimated, rather than calculated by mode projection integrals as in §A.1, since the actual velocities during the impulsive tilt were unknown, rendering further precision in this part of the calculation unproductive. Therefore, the free mode response was estimated by assuming that the `impulsive' velocity initially imparted to the fluid during the tilt-out later gets represented by a freely oscillating (1,1,1) mode. The impulsive velocity (in tank co-ordinates) owing to the tilt was estimated, together with the velocity due to the Coriolis force acting over this period, from the calibrations in Manasseh (1991). This estimate was made near the tank ends (where it is a maximum) and matched by a freely oscillating (1,1,1) mode with appropriate amplitude and phase to account for the estimated velocity at the ends.
At time t=0 the particles are located on a hypothetical wire at 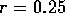 ,
,
 and parallel to the
and parallel to the  -axis. The integrations were performed to
a nondimensional time of 5 revolutions. The timelines corresponding to the loci
of the positions of a succession of particles were also calculated. A line has
been plotted at t=0 to mark the wire. Timelines have been plotted at
-axis. The integrations were performed to
a nondimensional time of 5 revolutions. The timelines corresponding to the loci
of the positions of a succession of particles were also calculated. A line has
been plotted at t=0 to mark the wire. Timelines have been plotted at 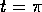 ,
and at each revolution thereafter, on the
,
and at each revolution thereafter, on the  -
- projection shown in
figure 3.
projection shown in
figure 3.
Further details on the calculation and cross-checks against other methods are in Manasseh (1991).
Aldridge, K.D. & Stergiopoulos, S. 1991 A technique for direct measurement of time-dependent complex eigenfrequencies of waves in fluids. Phys. Fluids A 3, 316-327.
Baker, J.D. 1966 A technique for the precise measurement of small fluid velocities. J. Fluid Mech. 26, 573-575.
Fultz, D. 1959 A note on overstability, and the elastoid-inertia oscillations of Kelvin, Solberg and Bjerknes. J. Meteorol. 16, 199-208.
Gledzer, E.B., Dolzhanskii, F.V. & Obukhov, A.M. 1989 Instability of elliptical rotation and simple models of vortex fluid flows. Abstracts, Euromech 245: The effect of background rotation on fluid motions, Dept. Applied Math. & Theor. Physics, Cambridge, Uk, April 10-13 1989.
Gledzer, E.B. & Ponomarev, V.M. 1992 Instability of bounded flows with elliptical streamlines. J. Fluid Mech. 240, 1-30.
Greenspan, H.P. 1968 The theory of rotating fluids. Cambridge University Press.
Gunn, J.S. & Aldridge, K.D. 1990 Inertial wave eigenfrequencies for a non-uniformly rotating fluid. Physics of Fluids A 2(11), 2055-2060.
Kelvin, Lord 1880 Vibrations of a columnar vortex. Phil. Mag. 10, 155-168.
Kudlick, M. 1966 The precessing cylinder. Phd. thesis, Massachusetts Institute of Technology.
Malkus, W.V.R. 1968 Precession of the Earth as the cause of geomagnetism. Science 160, 259-264.
Malkus, W.V.R. 1989 An experimental study of the global instabilities due to the tidal (elliptical) distortion of a rotating elastic cylinder. Geophys. Astrophys Fluid Dynamics,48, 123-134.
Malkus, W.V.R., Waleffe, F.A. 1991 Transition from order to disorder in elliptical flow: a direct path to shear flow turbulence. Advances in Turbulence 3, Editors: A.V. Johansson, P.H. Alfredsson, Springer-Verlag Berlin, Heidelberg, 197-203.
Manasseh, R. 1991 Inertia wave breakdown: experiments in a precessing cylinder. PhD thesis, University of Cambridge.
Manasseh, R. 1992 Breakdown regimes of inertia waves in a precessing cylinder. J. Fluid Mech. 243, 261-296.
Manasseh, R. 1993 Visualization of the flows in precessing tanks with internal baffles, American. Inst. Aeronautics and Astronautics J. 31, 312-318.
McEwan, A.D. 1970 Inertial oscillations in a rotating fluid cylinder. J. Fluid Mech. 40, 603-640.
McIntyre, M.E. Norton, W.A. 1990 Dissipative wave-mean interactions and the transport of vorticity or potential vorticity. J. Fluid Mech. 212, 403-435.
Scott, P.R., Tan, D.G.H. 1993 Complex-frequency method for computing the dynamics of liquid in a spinning container. J. Guidance, Control and Dynamics, 16(1), 190-196.
Stergiopoulos, S., Aldridge, K.D. 1982 Inertial waves in a fluid partially filling a cylindrical cavity during spin-up from rest. Geophys. & Astrophys. Fluid Dyn. 21, 89-112.
Tan, D.G.H. 1991 Dynamics of a rotating body containing a liquid-filled cavity. Final Report (Volume 2). Dept. Applied Math. & Theor. Physics, University of Cambridge.
Thompson, R. 1970 Diurnal tides and shear instabilities in a rotating cylinder. J. Fluid Mech. 40, 737-751.
Waleffe, F. 1990 On the three dimensional instability of strained vortices. Phys. Fluids A 2(1), 76-80.
Wood, W.W. 1966 An oscillatory disturbance of rigidly rotating fluid. Proc. Royal Soc. A 293, 181-212.
Distortions of inertia waves in a rotating fluid cylinder forced near its fundamental mode resonance
This document was generated using the LaTeX2HTML translator Version 0.6.4 (Tues Aug 30 1994) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html a113.tex.
The translation was initiated by on Mon Jan 9 15:19:05 EST 1995